• 表現論って何でしょう？
• 表現論にはどのような分野がありますか？
• 表現論の歴史について教えてください
• 表現論の入門書にはどんなものがありますか？
• 表現論の常識
• ネットから入手可能な表現論の初歩のお話
• 表現論に出てくる図形
• 日本語ホームページに戻る

表現論ってなんでしょう？

「表現論の研究をしています」というとよく一般の人からは「文学の研究かなんかですか？」ときかれます。でも

では表現論では何を研究するのでしょうか？ 数学では、 Lie 群とか対称群とか運動群といったように「群」と呼ばれる対象がよく現れますが、群は比較的わかりにくく抽象的な概念といえます。表現論ではこのわかりにくいものをわかりやすく「表現」することを目標にします。具体的には群の元を線形作用素（あるいは行列）で置き換えて考えるということになります。

さらにこれから派生して、群をベクトル空間で近似したもの(リー環と言います)の表現とか、 あるいは抽象的にある種の環(加法と乗法、二種類の演算を持った代数系)の表現なども考えたりします。 最近流行りなのは「量子群」と呼ばれる対象の表現論です。

目次に戻る

表現論にはどのような分野がありますか？

一口に 表現論 といってもその範囲は広く、様々な分野を含んでいます。代表的なものをあげますと

• Lie 群論、 Lie 環論
• フーリエ 解析、調和解析
• 対称空間の理論
• 不変式論
• 函数解析
• (表現論的)組み合わせ論
• 特殊函数論

目次に戻る

表現論の入門書にはどんなものがありますか？

何を目的として入門書を読むのか？ということにもよりますが、とりあえず日本語の入門書を紹介しておきます。もちろんこのリストは私の偏見の塊ですので、これがすべてだとか、本当に入門書だとか思うとえらい目に遭うこともあります。そういう目に遭っても私は一切責任をとりません。

より詳しいリストがこちらにあります。→ [表現論の教科書のページ]

• 岡本清郷, フーリエ解析の展望, すうがくぶっくす17, 朝倉書店, 1997.

  前半はフーリエ解析の復習を兼ねて、単位円（フーリエ級数）、実数（フーリエ変換）、球面（球関数展開）の３つの場合にそれぞれフーリエ変換、ポアッソン積分、佐藤超函数などの基本的な事項を解説してあります。この部分は表現論的な視点は極力押えてあるようです。
  このあと「フーリエ解析の背景」として等質空間上の解析とポアッソン積分の一般化についての入門的な解説がなされています。この部分は表現論的な解説です。
  この他、ファインマンの経路積分やカッツムーディリー環の表現など岡本先生の最近の仕事に関係する話題がトピックス的に扱われています。この部分は初心者には難しいかも。

• 彌永昌吉・杉浦光夫、応用数学者のための代数学、岩波書店, 1960.

  とっても古い本ですが、この本で有限群の表現論の初歩を勉強しました。「応用数学者のための」とは書かれていますが、あまりその方面は扱われていません。ヤング図形とか対称群の表現論の詳しいことを知りたいけれど、線型代数の初歩程度の知識しかないという人にお勧め。ある程度知識のある人は第3章から読めば良いでしょう。

• 佐武一郎、代数学への誘い、遊星社

  第１、２章で群の概念について解説され、そのあと第３章では群の表現と双対性について解説されている。そこには自然とフーリエ変換、ガウス和、テータ函数などが登場していておもしろい。ここまでで６３ページしかなく、絶好の入門書といえるかもしれない。

  本書の主題は実は第３章以降で (^^;;、そこでは二次体の整数論を軽く解説したあと円分体の整数論にまで話が及んでいる。本論の外では世間話のような感じで「類体論とはどのようなものか？」というようなことまで解説されている。学部の３回生ぐらいが読むのにちょうどよい（？２回生ぐらいの方がいいかなぁ？）、楽しめる本です。おすすめ。

• 堀田良之、加群十話−代数学入門−、すうがくぶっくす３、朝倉書店

  線形代数の初歩から書き起こして、対称群、有限群の表現論が面白くまとめられてます。 Young 図形 がたくさんでてくるのも嬉しいですね。最後は D -加群の話まで行ってしまいます。 表現というよりは「加群」という考え方が自然と身につく良い本だと思います。 堀田先生の語り口はシャイでいるようでいて大胆で、そのアンバランスさが何とも好きです。

• 山内恭彦・杉浦光夫、連続群論入門、新数学シリーズ１８、培風館、1966

  二次または三次の行列群を例にとってその Lie 群としての構造、既約有限次元表現の話などが詳しく述べられている。回転群の表現論の絶好の入門書。直交多項式、微分方程式などの話も自然に出てくるように書かれており、球函数の話なども興味深く展開されている。しかしこれが1966年ですからねー。この分量でここまで書いてあるのはすごい本だと思います。

• 神保道夫、量子群とヤン・バクスター方程式、シュプリンガー現代数学シリーズ、シュプリンガーフェアラーク東京、1990

  今話題の量子群の構造とか理論的な背景、表現についてわかりやすく書いてあります。ここで扱われている量子群は一般線形群（の Lie 環）の量子変形で、古典的な Schur の相互律の量子化などについても書かれています。 改訂版とは書かれていませんが、こまめに文献表などを追加されているようです。

表現論の日本語の入門書 で簡単かつおもしろいものは未だ少ないと思います。 海外ではたくさんの教科書 が出ているので特に若い人のためにはこの状況は改善されるべきでしょう。

目次に戻る

表現論の常識

目次に戻る

ネットから入手可能な表現論のノート

1. NEW!! [00/11/25 16:36]

   表現論の方法と考え方 (by 西山 享: 京都大学 総合人間学部)
   [名古屋大学 ('00/11) での集中講義ノート]

   初歩的な代数学(群論、環論、体論)の知識と、線型代数学の知識があれば、無理なく読めるように書きました。 前半は有限群の表現の話ですが、すべてコンパクト群とか代数群の表現に使える形になるように努めています。 特に、球関数とか、ヘッケ環の話とかが普通の教科書ではあまり見当たらないかと思います。 後半は一般線型群の話から始めて、直交群の表現(球面調和多項式)の話までを解説しました。 不変式論の初歩の初歩を扱った入門書としても読めると思います。

   PDF file : ; Post Script file : ; TeX dvi file : ; [ ]

2. 対称群の表現 -- 対称式と調和多項式 -- (西山 享: 京都大学 総合人間学部)

   [目次]

   • 群とあそぼう（復習）
   • 対称群の作用する空間
   • 線型群のお話
   • 対称式と調和多項式
   • 多項式環上の対称群の表現

   [計 50 ページ]('98/1/5)

   Post Script file : ; TeX dvi file :

3. リー群の軌道分解 (松木敏彦: 京都大学 総合人間学部)

   [目次]

   • 群論
   • 線型代数
   • O(p) × O(q) \ O(n) / O(r) × O(s)
   • リー群とリー環入門
   • 対称空間
   • 主定理 (コンパクトの時)
   • ルート系

   [計 31 ページ]('98/3)

   TeX dvi file : 松木さんのホームページ

4. 半単純 Lie 群の standard 表現入門 -- $ Sp(2, \R) $ と $ SU(2, 2) $ を中心に --, 数理研講究録909所収. (西山 享: 京都大学 総合人間学部)

   こちらは数学の専門家向けです。半単純リー群の表現論をこれから学ぶ研究者のために書きました。したがって表現論の専門家向けではありません。

   PDF file : ; Post Script file : ; TeX dvi file :

目次に戻る

---

表現論に出てくる図形

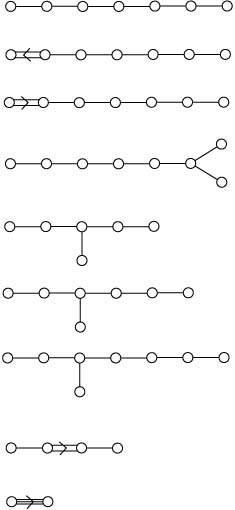
表現論で良く出てくる図形に Dynkin 図形と Young 図形があります。親戚筋として拡大 Dynkin 図形、佐武図形、 skew Young 図形などもありますね。

Dynkin 図形



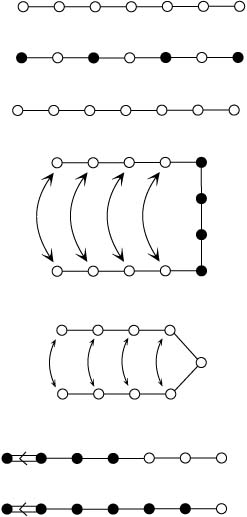
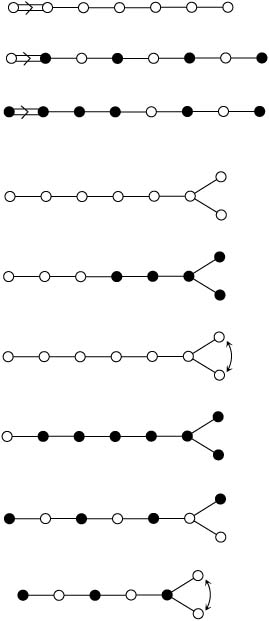
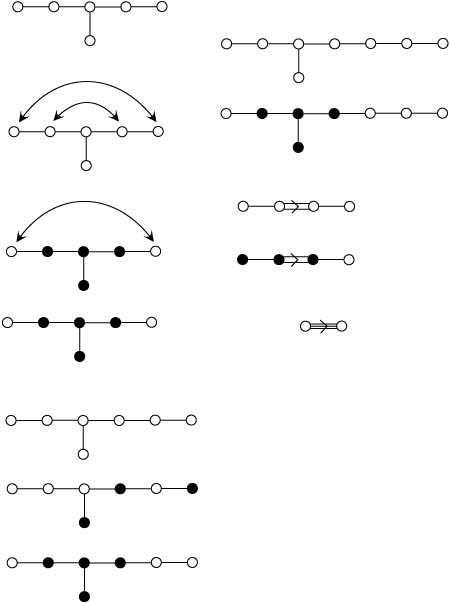
A, B 型の佐武図形	C, D 型の佐武図形	E, F, G 型の佐武図形

目次に戻る

---

日本語ホームページに戻る

Last Update :